Each week, Mr Sibachir, on behalf of the Mathematics Department, circulates a set of Maths Challenges for the School community. Here, he presents us with a series of problems which have proved most intriguing, enjoyable or challenging to pupils and staff alike. The solutions proposed by pupils will be published in the next edition of House.
- Finn, Lorenzo and Elliot run in a 100m race. When Finn finishes, Lorenzo is 16m behind him and when Lorenzo finishes, Elliot is 25m behind him. The boys run at constant speeds throughout the race.
How far behind was Elliot when Finn finished?
- Mr Head goes into a supermarket and buys three items. It has been a while since he has used a calculator and he multiplies the cost (in pounds, using the decimal point for the pence) instead of adding them. At the checkout he says, “So that’s £5.88” and the checkout attendant, correctly adding the items, agrees. Can you find the values of the three items?
- Every Tuesday, Mrs Meyer leaves home at 6:30pm and drives to her fitness class.
If she drives at an average speed of 20 miles per hour, she arrives 3 minutes late. If she drives at an average speed of 30 miles per hour, she arrives 3 minutes early.
What average speed should she drive at to arrive on time?
-
I keep three circular medallions in a rectangular box in which they just fit with each one touching the other two. The smallest one has radius 4cm and touches one side of the box, the middle sized one has radius 9cm and touches two sides of the box, and the largest one touches three sides of the box. What is the radius of the largest one?
- A circle of the radius 1cm is inscribed in an equilateral triangle. A smaller circle is inscribed at each vertex touching the first circle and tangent to the two ‘containing’ sides of the triangle. This process is continued ad infinitum…
What is the sum of the circumferences of all the circles?
-
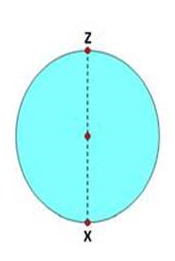The figure shows a circular lake. Points X and Z are located across the lake from each other such that XZ is a diameter of the circular lake. Carlos is standing at point X and wants to travel as quickly as he can to point Z by walking and/or running. He can walk twice as fast as he can swim. What should Carlos do?
